기초통계 #4 정규분포

* 정규분포 : 중심을 나타내는 평균과 산포를 의미하는 표준편차에 의해 형태가 결정되는 분포

(많은 분야에서 연속형 변수로서 나타나는 현상을 표현하는 확률모형으로 사용되면서 정규 분포라고 불리게 되었다고 합니다.)

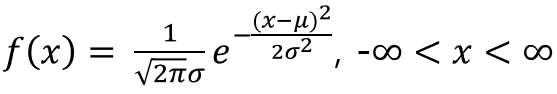
평균이 μ이고 표준편차가 σ인 정규분포 그래프 예시

어떤 확률현상이 정규 분포를 따른다고 할 때 평균(μ)과 표준편차(σ)에 따라서 아래와 같은 특성을 따른다.

[특성1]

- 이 현상의 한 관찰값이 P(μ-1σ < X < μ+1σ)에서 나타날 확률이 0.6826

- 이 현상의 한 관찰값이 P(μ-2σ < X < μ+2σ)에서 나타날 확률이 0.9544

- 이 현상의 한 관찰값이 P(μ-3σ < X < μ+3σ)에서 나타날 확률이 0.9974

 

 

 

* 표준정규분포 : 평균이 0이고, 표준편차가 1인 정규분포 N(0,1)

(개체의 관찰값과 평균의 차이를 표준편차로 나눈 값으로 표준화한 분포)

예시. 평균이 100이고 표준편차가 10인 정규분포에서 120이상일 확률은 표준화 시 Z=(120-100)/10=2가되어 표준정규 분포에서 2이상인 확률을 구하는 것과 같다.

 

특성1을 Z로 변형하면 아래와 같은 특성을 따른다.

- P(μ-1σ < X < μ+1σ) => - P(-1< Z=((X-μ)/σ) < 1)=0.6826

- P(μ-2σ < X < μ+2σ) => - P(-2< Z=((X-μ)/σ) < 2)=0.9544

- P(μ-3σ < X < μ+3σ) => - P(-3< Z=((X-μ)/σ) < 3)=0.9974